内存优化技术
首先,如果用4bit量化,时间换空间实现了,推理速度也会相应的下降很多。因此,如果GPU充足,最好可以在训练的时候用fp16精度加载参数,时间会相对快很多,24GB勉强够用。(2024年5月7日感悟)
当然,业界还有一些其他的内存优化技术,比如Colossal-AI和LoRA。它们各有特点,相比之下,
GaLore,Gradient Low-Rank Projection,梯度低秩投影优势在于它既能支持全量更新,实现从头开始的完整预训练,又能显著降低内存占用,让普通消费级硬件也能训练大模型。这种全面而均衡的能力提升,是其他内存优化技术难以企及的。在论文中,研究人员使用70亿参数的LLaMA语言模型对GaLore进行了评估。结果显示,正常BF16精度训练LLaMA 7B模型,需要58GB显存。使用GaLore方法,结合8位量化优化器和逐层权重更新技术后,优化器状态的内存占用降低了65.5%,从42GB减少到了14.5GB。模型参数内存为14GB不变,但由于大幅降低了优化器状态和激活内存占用,最终总内存消耗仅为21.3GB。原文
Colossal-AI是一个支持分布式训练的框架。它通过数据并行、张量并行等策略,将大模型切分成多个部分,分散到不同的设备上训练。但这并没有减少训练的总内存需求,只是将压力分摊到了多个设备上。原文
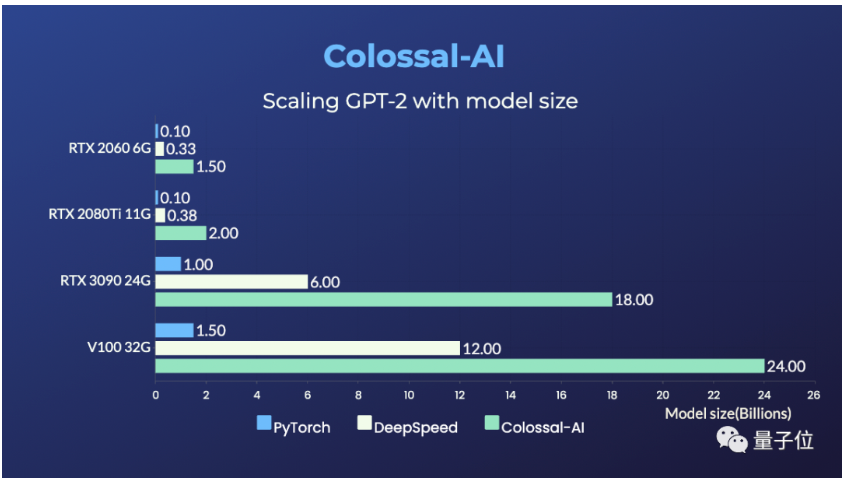
LoRA则是在预训练模型的基础上,叠加一个小的低秩矩阵进行训练。这种方法减少了微调阶段需要更新的参数数量,但它的内存优势仅限于微调阶段,对预训练阶段无效。
模型量化剪枝-vLLM
直接llama,通过quantization能将模型压缩,提升推理速度。
What is 4-bit Quantization for Llama2 ?
Quantization in the context of deep learning is the process of constraining the number of bits that represent the weights and biases of the model. Weights and Biases numbers that we need in backpropagation.
In 4-bit quantization, each weight or bias is represented using only 4 bits as opposed to the typical 32 bits used in single-precision floating-point format (float32).
Why does it use less GPU Memory?
The primary advantage of using 4-bit quantization is the reduction in model size and memory usage. Here’s a simple explanation:
A float32 number takes up 32 bits of memory. A 4-bit quantized number takes up only 4 bits of memory. So, theoretically, you can fit 8 times more 4-bit quantized numbers into the same memory space as float32 numbers. This allows you to load larger models into the GPU memory or use smaller GPUs that might not have been able to handle the model otherwise.
The amount of memory used by an integer in a computer system is directly related to the number of bits used to represent that integer.
Memory Usage for 4-bit Integer: A 4-bit integer uses 4 bits of memory.
Memory Usage for 32-bit Integer: A 32-bit integer uses 32 bits of memory.
Conversion to Bytes To convert these to bytes (since memory is often measured in bytes):
1 byte = 8 bits A 4-bit integer would use ( 4/8 = 0.5 ) bytes. A 16-bit integer would use ( 16/8 = 2 ) bytes.、
4 bit Will make the accuracy lower due to the quantification.
: `import numpy as np
# Simulate original float32 weights
original_weights = np.random.rand(1000).astype(np.float32)
# Simulate 4-bit quantized weights
# First, normalize the weights to a range of 0 to 15 (since 4 bits can represent 16 values)
`quantized_weights = np.round(original_weights * 15).astype(np.uint8)
# De-normalize to get the approximated original weights
approximated_weights = quantized_weights / 15.0
# Calculate the error
error = np.abs(original_weights - approximated_weights).mean()
`print(f”Average Quantization Error: {error}”)
`original_weights
`quantized_weights
Tools and tutorials for 4bit integration?
pip install bitsandbytesIn this notebook, we will learn together how to load a model in 4bit, understand all its variants and how to run them for inference.
In the training notebook, you will learn how to use 4bit models to fine-tune these models.
If you liked the previous work for integrating LLM.int8, you can have a look at the introduction blogpost to lean more about that quantization method.
Note that this could be used for any model INCLUDING GPT that supports device_map (i.e. loading the model with accelerate) - meaning that this totally agnostic to modalities, you can use it for Blip2, etc.